Joule Thomson Theory for Liquid Nitrogen Cooling
The Joule-Thomson effect is a change in temperature that accompanies the expansion of a gas without production of work or transfer of heat. At ordinary temperatures and pressures, all real gases except hydrogen and helium cool upon such expansion; this phenomenon often is utilized in liquefying gases. The phenomenon was investigated in 1852 by the British physicists James Prescott Joule and William Thomson (Lord Kelvin).
The first law of thermodynamics states that the change of heat is equal to the change of internal energy plus work done by the gas. This is expressed as
Q = ΔU + W
Joule took two copper vessels and connected them with a gas valve. Vessel A was filled with compressed air to 21 atmospheres and B was exhausted to a condition of a vacuum. The assembly was immersed in a water bath with a thermometer. After reaching a steady-state temperature, the gas valve was opened and the air from A expanded into B until a new pressure was reached. During the process no change in temperature was observed.
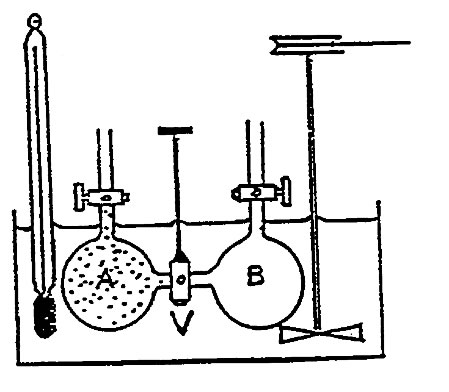
No work transfer occurred because the air expanded into a vacuum. Thus,
W = 0
Also, no heat was transferred.
Q = 0
This leaves us with
ΔU = 0
In Joule's words, "no change of temperature occurs when air is allowed to expand in such a manner as not to develop mechanical power". Because the enthalpy is the same, this process is isenthalpic.
If this is the case, one must ask how can this throttling effect result in the cooling of a gas if the temperature is not suppose to change. The answer is that the above follows for an ideal gas, where molecular attraction is negligible, and no gas is truly ideal. The fact that one can liquefy a gas attests to this fact. The truth is that the temperature of a real gas may increase or decrease, depending on whether or not the throttling occurs above or below the inversion temperature.
On one hand, as a real gas expands the average distance between molecules grows. Because of intermolecular attractive forces, expansion causes an increase in the potential energy of the gas. If no external work is extracted in the process and no heat is transferred, the total energy of the gas remains the same because of the conservation of energy. The increase in potential energy thus implies a decrease in kinetic energy and therefore in temperature.
A second mechanism has the opposite effect. During gas molecule collisions, kinetic energy is temporarily converted into potential energy. As the average intermolecular distance increases, there is a drop in the number of collisions per time unit, which causes a decrease in average potential energy. Again, total energy is conserved, so this leads to an increase in kinetic energy (temperature).Below the Joule–Thomson inversion temperature, the former effect (work done internally against intermolecular attractive forces) dominates, and free expansion causes a decrease in temperature. Above the inversion temperature, gas molecules move faster and so collide more often, and the latter effect (reduced collisions causing a decrease in the average potential energy) dominates: Joule–Thomson expansion causes a temperature increase.
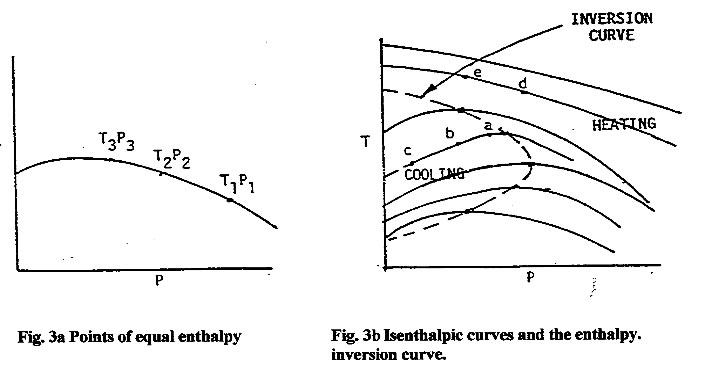
Below are families of curves showing different enthalpy values at various pressures and temperatures. In order for cooling to occur, one must drop the pressure below the inversion point (curve maximum); otherwise, the temperature will increase as shown by curves D and E.
Let’s take a closer look at throttling with a real gas. Below we have a pipe with a porous plug that develops a higher pressure P1 to the left that drives a small volume, V1, through the plug. This acts like a virtual piston performing work, P1V11, on the gas. On the right, another virtual piston expands, performing work, V2P2, by the gas. This time, there is no free expansion; the gas expands against gas on the other side of the plug.

Going back to our formula,
U2 – U1 = P1V1 – P2V2
and knowing that for most gases P2V2 > P1V1, we see there is a decrease in the internal energy of the gas,
ΔU < 0
Joule’s determined that the internal energy is dependent only on temperature. Thus, the temperature of the gas decreases.